Skip to main content

2. 向量(Vector): 一维数组

本文参考:

  1. NumPy Illustrated: The Visual Guide to NumPy
  2. A Visual Intro to NumPy and Data Representation
  3. 《Python Data Science Handbook》

向量在NumPy中用一维数组表示。

1. 向量初始化​

通过Python列表可以创建NumPy数组，如下将列表元素转化为一维数组：

danger

注意，确保列表元素类型相同，否则dtype=’object'，将影响运算甚至产生语法错误。

由于在数组末尾没有预留空间以快速添加新元素，NumPy数组无法像Python列表那样增长，因此，通常的做法是在变长Python列表中准备好数据，然后将其转换为NumPy数组，或是使用np.zeros或np.empty预先分配必要的空间：

通过以下方法可以创建一个与某一变量形状一致的空数组：

不止是空数组，通过上述方法还可以将数组填充为特定值：

在NumPy中，还可以通过单调序列初始化数组：

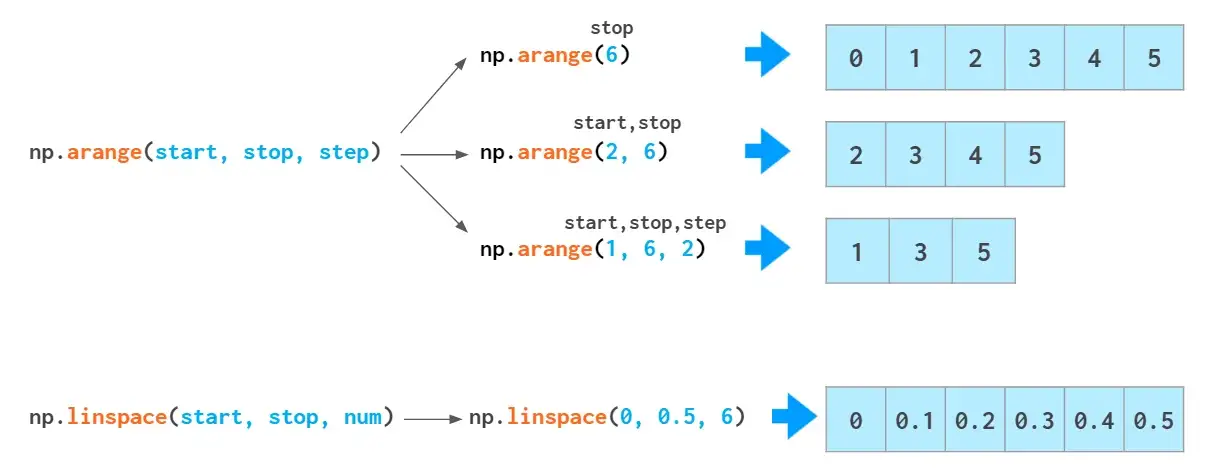
如果您需要[0., 1., 2.]这样的浮点数组，可以更改arange输出的类型，即arange(3).astype(float)，但有更好的方法：由于arange函数对类型敏感，因此参数为整数类型，它生成的也是整数类型，如果输入float类型arange(3.），则会生成浮点数。

arange浮点类型数据不是非常友好：

上图中，0.1对我们来说是一个有限的十进制数，但对计算机而言，它是一个二进制无穷小数，必须四舍五入为一个近似值。因此，将小数作为arange的步长可能导致一些错误。可以通过以下两种方式避免如上错误：一是使间隔末尾落入非整数步数，但这会降低可读性和可维护性；二是使用linspace，这样可以避免四舍五入的错误影响，并始终生成要求数量的元素。但使用linspace时尤其需要注意最后一个的数量参数设置，由于它计算点数量，而不是间隔数量，因此上图中数量参数是11，而不是10。

随机数组的生成如下：

There’s also a new interface for random arrays generation. It is:

  • better suited for multi-threading,
  • somewhat faster,
  • more configurable (you can squeeze even more speed or even more quality by choosing a non-default so-called ‘bit generator’),
  • able to pass two tricky synthetic tests that the old version fails. New-style random numbers generation

2.向量索引​

对于数组数据的访问，numpy提供了便捷的访问方式：

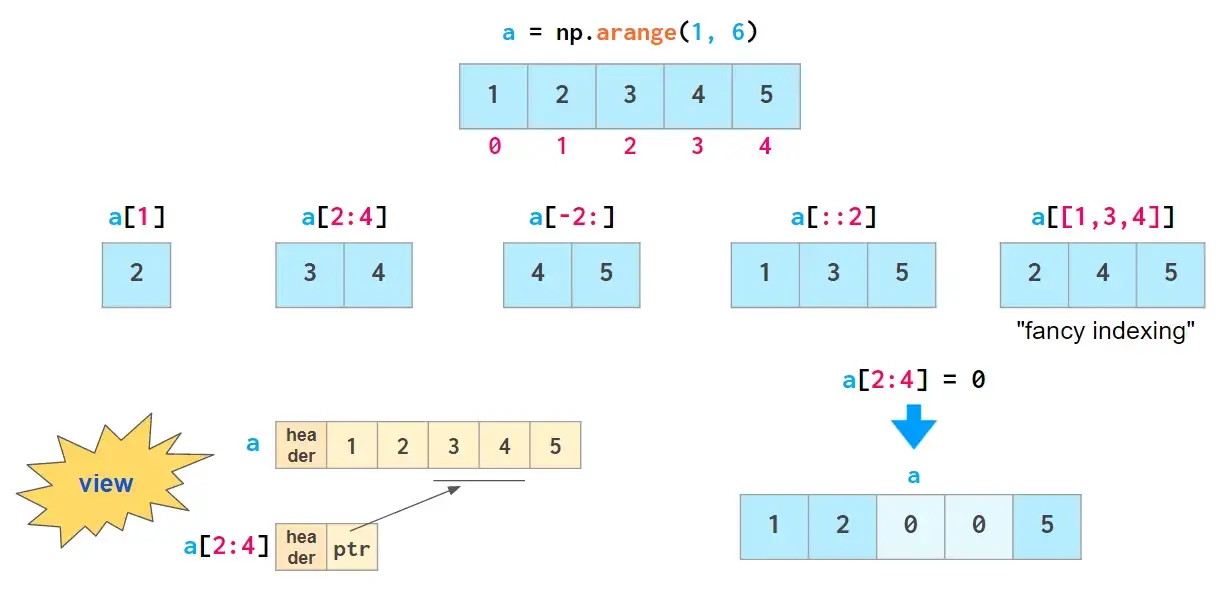
上图中，除“fancy indexing”外，其他所有索引方法本质上都是views：它们并不存储数据，如果原数组在被索引后发生更改，则会反映出原始数组中的更改。

上述所有这些方法都可以改变原始数组，即允许通过分配新值改变原数组的内容。这导致无法通过切片来复制数组：

Also, such assignments must not change the size of the array, so tricks like won’t work in NumPy — use np.insert, np.append, etc. instead (described in the “2D” section below).

此外，还可以通过布尔索引从NumPy数组中获取数据，这意味着可以使用各种逻辑运算符：

danger

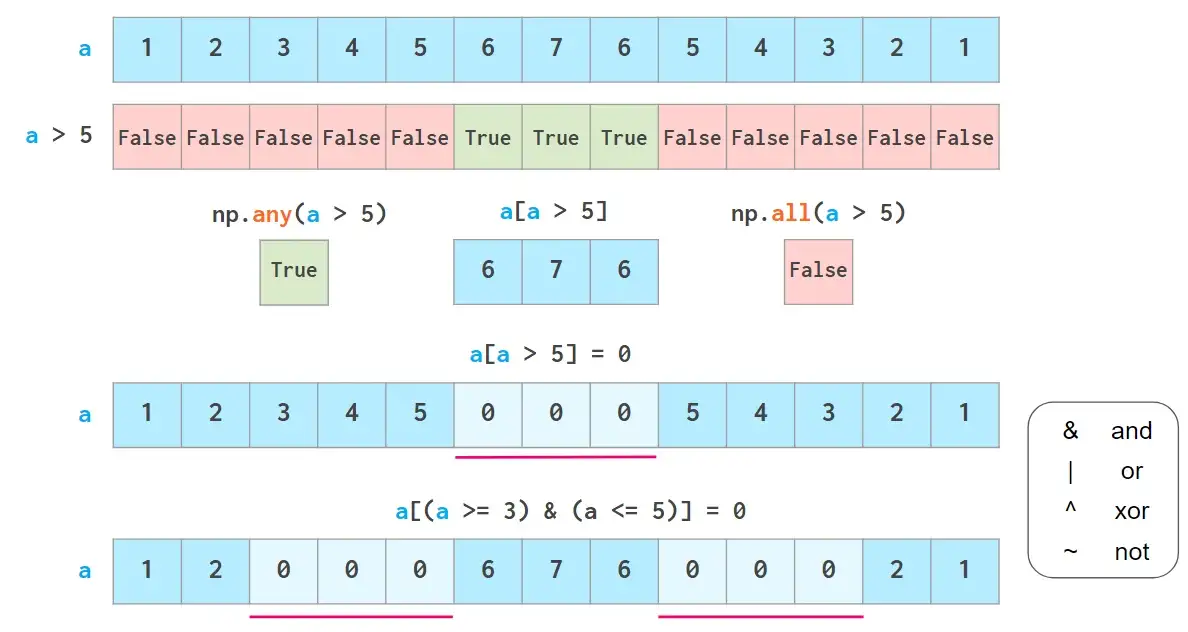
注意，不可以使用3 <= a <= 5这样的Python“三元”比较。

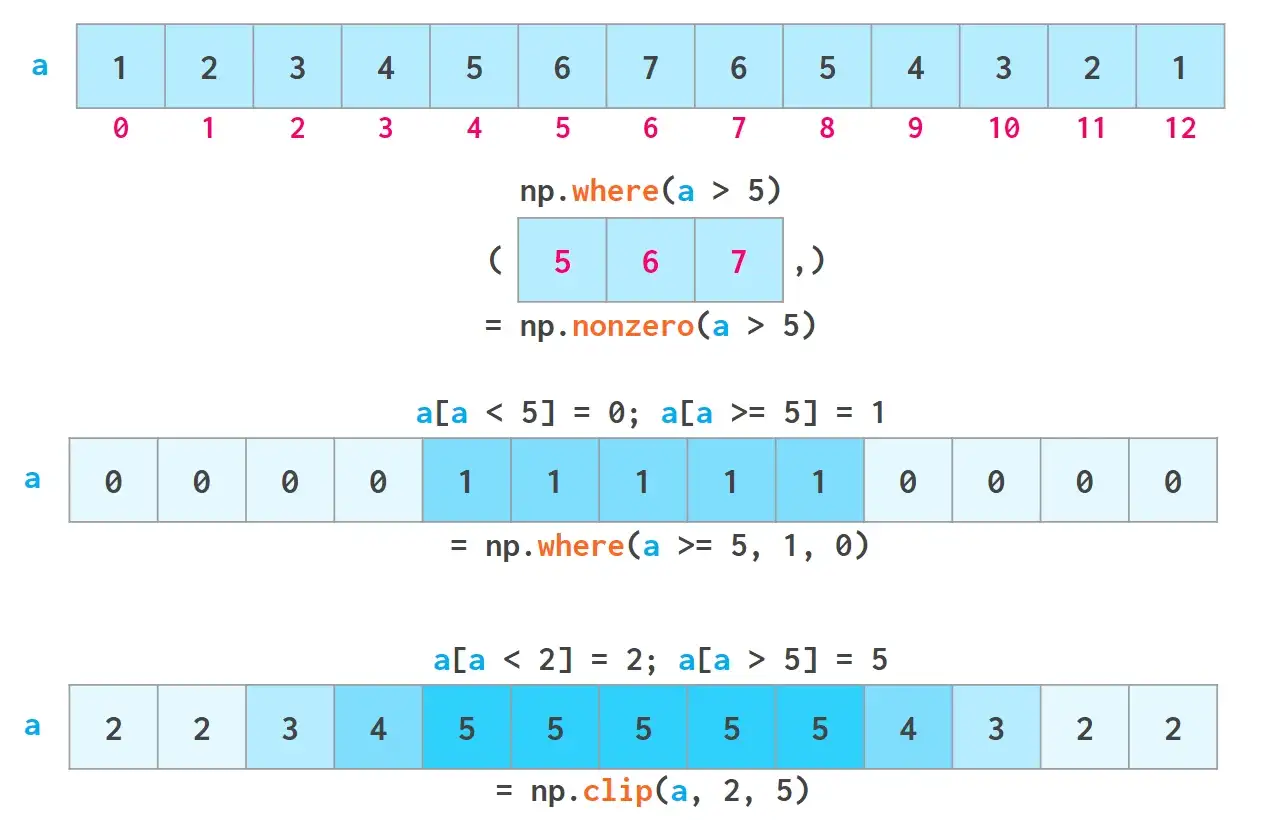
如上所述，布尔索引是可写的。如下图np.where和np.clip两个专有函数。

3.向量操作​

NumPy的计算速度是其亮点之一，其向量运算操作接近C++级别，避免了Python循环耗时较多的问题。NumPy允许像普通数字一样操作整个数组：

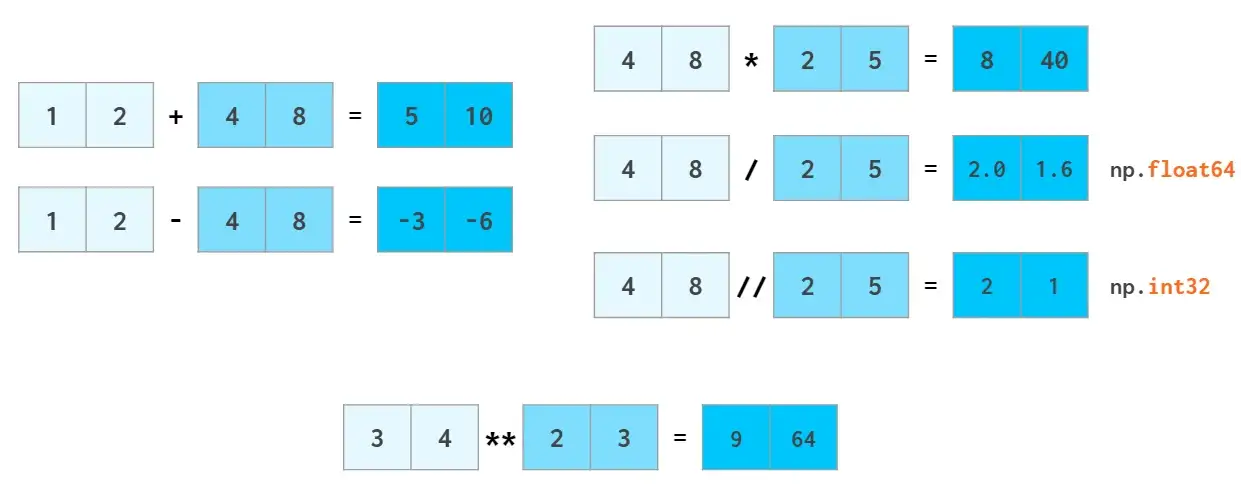
浮点数的计算也是如此，numpy能够将标量广播到数组：

numpy提供了许多数学函数来处理矢量：

向量点乘（内积）和叉乘（外积、向量积）如下：

numpy也提供了如下三角函数运算：

数组整体进行四舍五入：

tip
  1. floor向上取整
  2. ceil向下取整
  3. round四舍五入

np.around与np.round是等效的，这样做只是为了避免 from numpy import *时与Python aroun的冲突（但一般的使用方式是import numpy as np）。当然，你也可以使用a.round()。

numpy还可以实现以下功能：

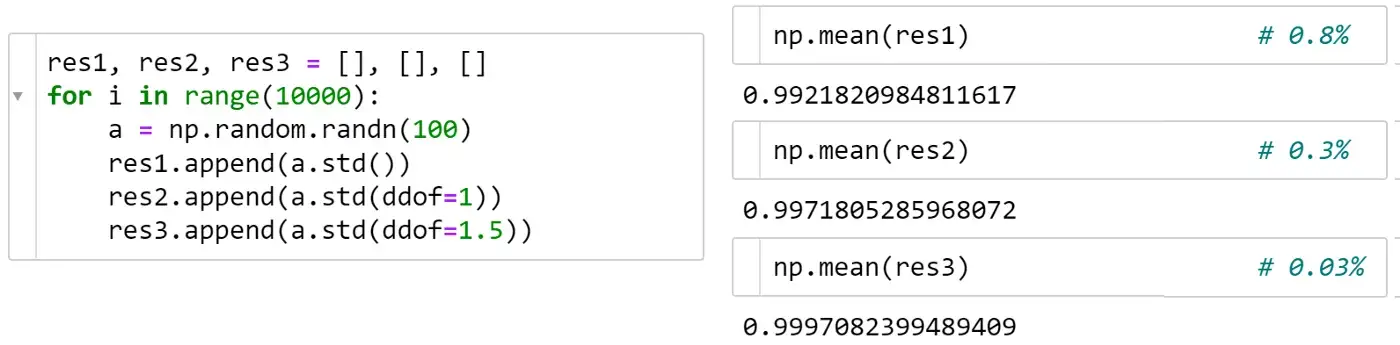
As you can see from the formula above, both std and var ignore Bessel’s correction and give a biased result in the most typical use case of estimating std from a sample when the population mean is unknown. The standard approach to get a less biased estimation is to have n-1 in the denominator, which is done with ddof=1 (‘delta degrees of freedom’):

The effect of the Bessel’s correction quickly diminishes with increasing sample size. Also, it is not a one-size-fits-all solution, e.g. for the normal distribution ddof=1.5 is better:

在numpy中，排序函数功能有所阉割：

对于一维数组，可以通过反转结果来解决reversed函数缺失的不足，但在2维数组中该问题变得棘手。

4.查找向量中的元素​

不同于Python列表，NumPy数组没有索引方法。

info
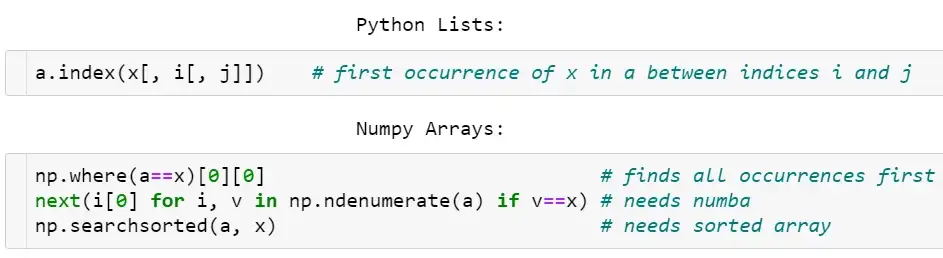
  • 可以通过np.where(a==x)[0][0]查找元素，但这种方法很不pythonic，哪怕需要查找的项在数组开头，该方法也需要遍历整个数组。
  • 使用Numba实现加速查找，next((i[0] for i, v in np.ndenumerate(a) if v==x), -1)，在最坏的情况下，它的速度要比where慢。
  • 如果数组是排好序的，使用v = np.searchsorted(a, x); return v if a[v]==x else -1时间复杂度为O(log N)，但在这之前，排序的时间复杂度为O(N log N)。

实际上，通过C实现加速搜索并不是困难，问题是浮点数据比较。

5.浮点数比较​

np.allclose(a, b)用于容忍误差之内的浮点数比较。

info
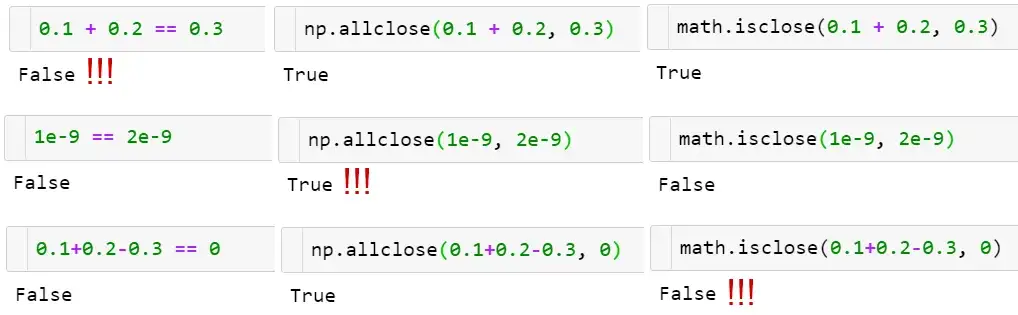
  • np.allclose假定所有比较数字的尺度为1。如果在纳秒级别上，则需要将默认atol参数除以1e9：np.allclose(1e-9,2e-9, atol=1e-17)==False。
  • math.isclose不对要比较的数字做任何假设，而是需要用户提供一个合理的abs_tol值（np.allclose默认的atol值1e-8足以满足小数位数为1的浮点数比较，即math.isclose(0.1+0.2–0.3, abs_tol=1e-8)==True。

此外，对于绝队偏差和相对偏差，np.allclose依然存在一些问题。例如，对于某些值a、b， allclose(a,b)!=allclose(b,a)，而在math.isclose中则不存在这些问题。查看GitHub上的浮点数据指南和相应的NumPy问题了解更多信息。