3. 矩阵(Matrix): 二维数组
本文参考:
- NumPy Illustrated: The Visual Guide to NumPy
- A Visual Intro to NumPy and Data Representation
- 《Python Data Science Handbook》
矩阵在NumPy中用二维数组表示。
1.矩阵初始化
矩阵的初始化语法与向量类似:
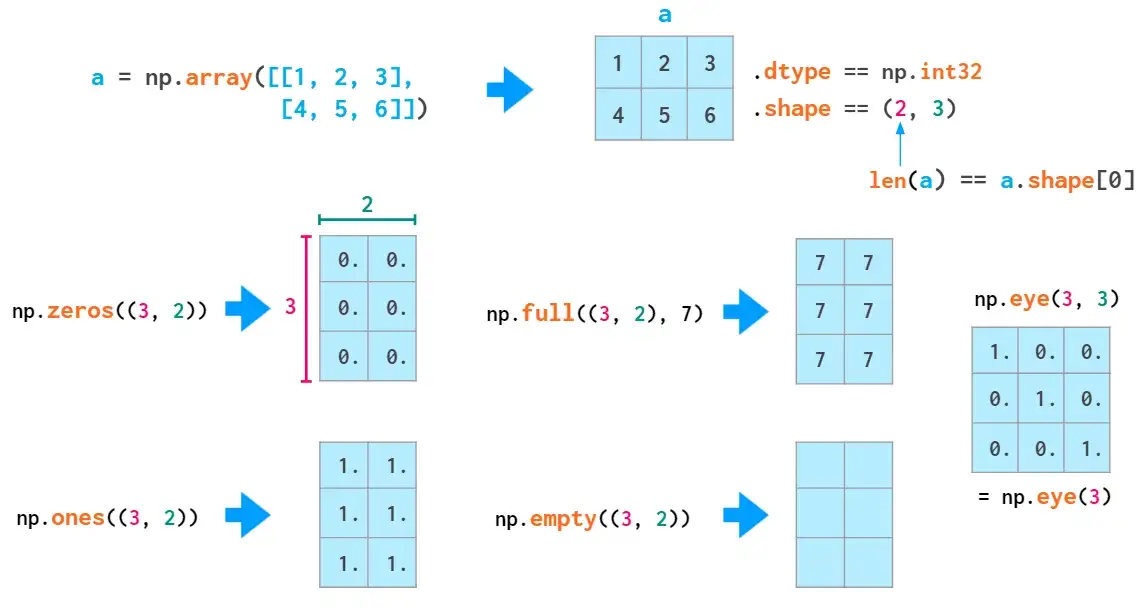
如上要使用双括号,因为第二个位置参数(可选)是为dtype(也接受整数)保留的。
随机矩阵的生成也与向量类似:

The ubiquitous double parentheses found their way to the interface of the new-style (see details in the 1D section above) numbers generation routines so that as of today only in np.eye has beauty taken prevelence over stringency and convenience of passing shapes as is:

二维数组的索引语法要比嵌套列表更方便:

“view”表示数组切片时并未进行任何复制,在修改数组后,相应更改也将反映在切片中。
2.轴参数
在求和等操作中,NumPy可以实现跨行或跨列的操作。为了适用任意维数的数组,NumPy引入了axis的概念。axis参数的值实际上就是维度数量,如第一个维是axis=0 ,第二维是axis=1,依此类推。因此,在2维数组中,axis=0指列方向,axis=1指行方向。
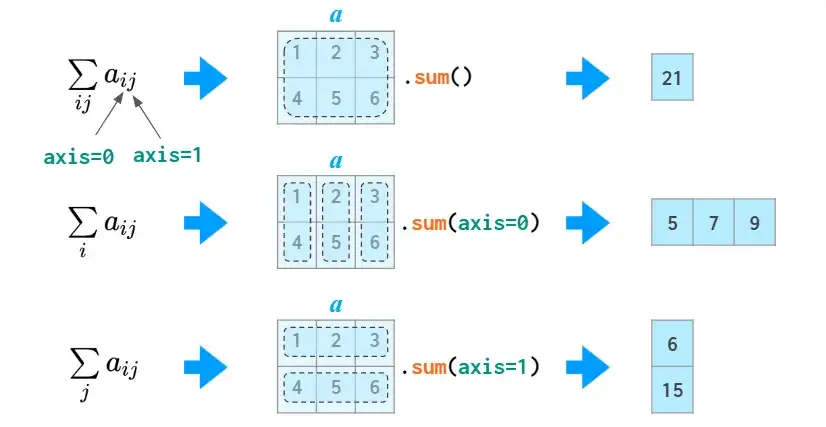
Generally speaking, the first dimension i (axis=0) is responsible for indexing the rows, so sum(axis=0) should be read like “for any given column sum over all of its rows” rather than just “column-wise”. The 2D case is somewhat counter-intuitive: you need to specify the dimension to be eliminated, instead of the remaining one you would normally think about. In higher dimensional cases this is more natural, though: it’d be a burden to enumerate all the remaining dimensions if you only need to sum over a single one.
The notion of the ‘axis’ argument (called ‘dimension’ in MATLAB) is actually very simple: it is just number of the index you want the operation to carry over. It is used in many functions in NumPy so it pays off to understand it, but if for some reason it doesn’t work out for you, in this particular case you can use the Einstein summation — that’s a way to do the sums without ‘axes’: np.einsum(‘ij->j’, a) is summing column-wise (same as sum(axis=0) in the image above) and np.einsum(‘ij->i’, a) is row-wise (same as sum(axis=1)).
3.矩阵运算
除了+,-,*,/,//和**等数组元素的运算符外,numpy提供了@运算符计算矩阵乘积:
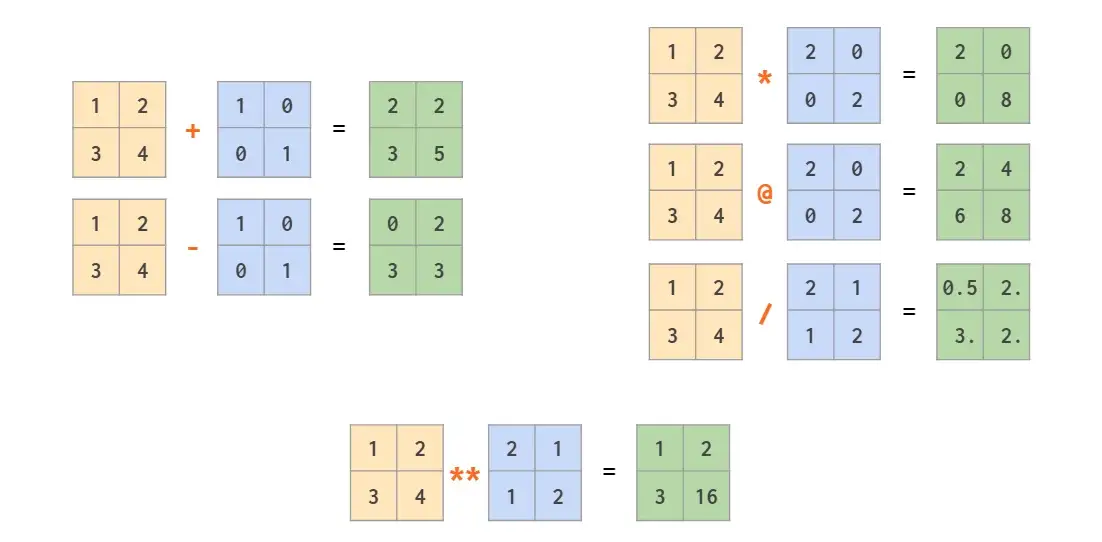
numpy同样可以通过广播机制实现向量与矩阵,或两个向量之间的混合运算:

注意,上图最后一个示例是对称的逐元素乘法。使用矩阵乘法@可以计算非对称线性代数外积,两个矩阵互换位置后计算内积:
4.行向量与列向量
根据前文可知,在2维数组中,行向量和列向量被区别对待。通常NumPy会尽可能使用单一类型的1维数组(例如,2维数组a的第j列a[:, j]是1维数组)。默认情况下,一维数组在2维操作中被视为行向量,因此,将矩阵乘行向量时,使用形状(n,)或(1,n)的向量结果一致。有多种方法可以从一维数组中得到列向量,但并不包括transpose:
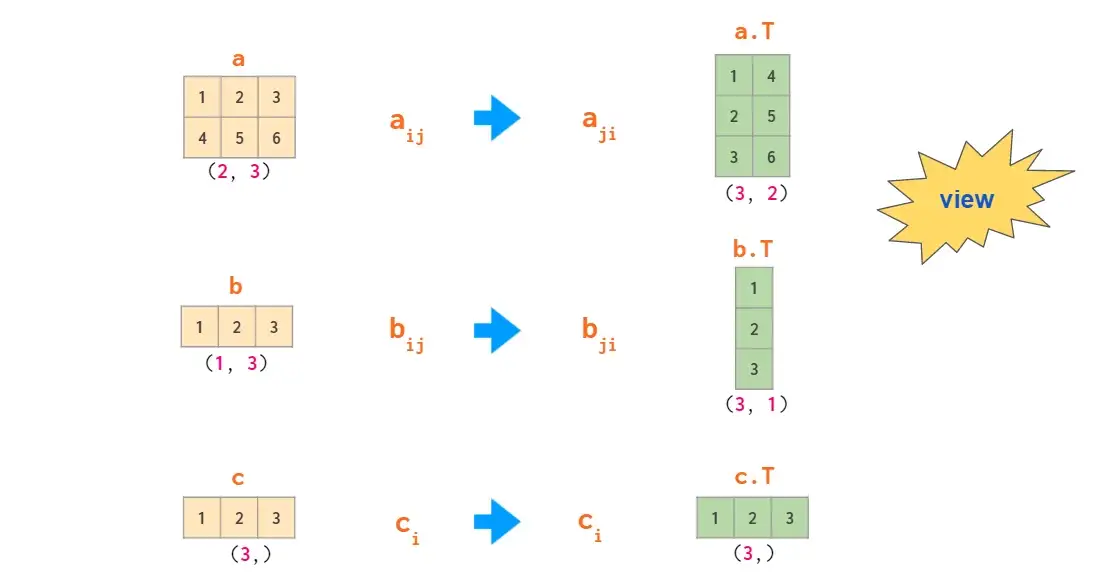
使用newaxis更新数组形状和索引可以将1维数组转化为2维列向量:
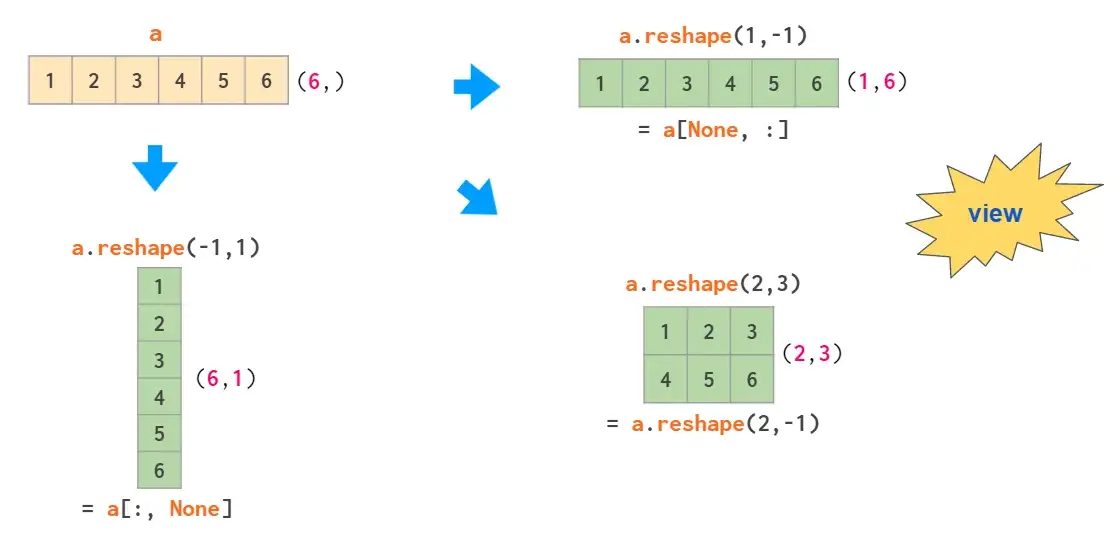
其中,-1表示在reshape是该维度自动决定,方括号中的None等同于np.newaxis,表示在指定位置添加一个空轴。
因此,NumPy中共有三种类型的向量:1维数组,2维行向量和2维列向量。以下是两两类型转换图:
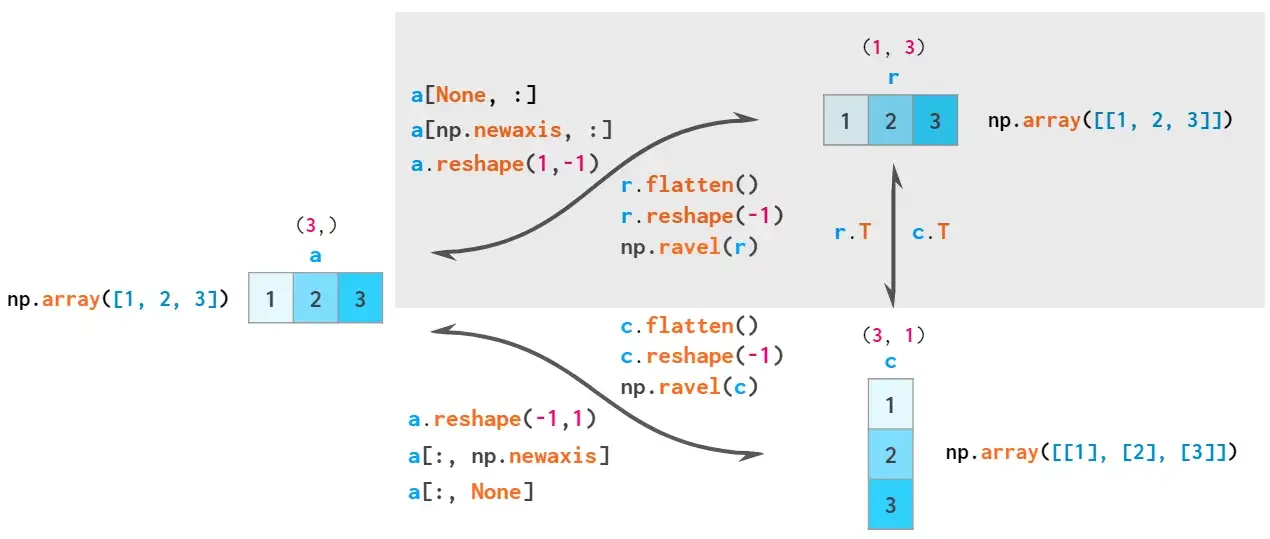
根据广播规则,一维数组被隐式解释为二维行向量,因此通常不必在这两个数组之间进行转换,对应图中阴影化区域。
严格来说,除一维外的所有数组的大小都是一个向量(如a.shape == [1,1,1,5,1,1]),因此numpy的输入类型是任意的,但上述三种最为常用。可以使用np.reshape将一维矢量转换为这种形式,使用np.squeeze可将其恢复。这两个功能都通过view发挥作用。
5.矩阵的操作
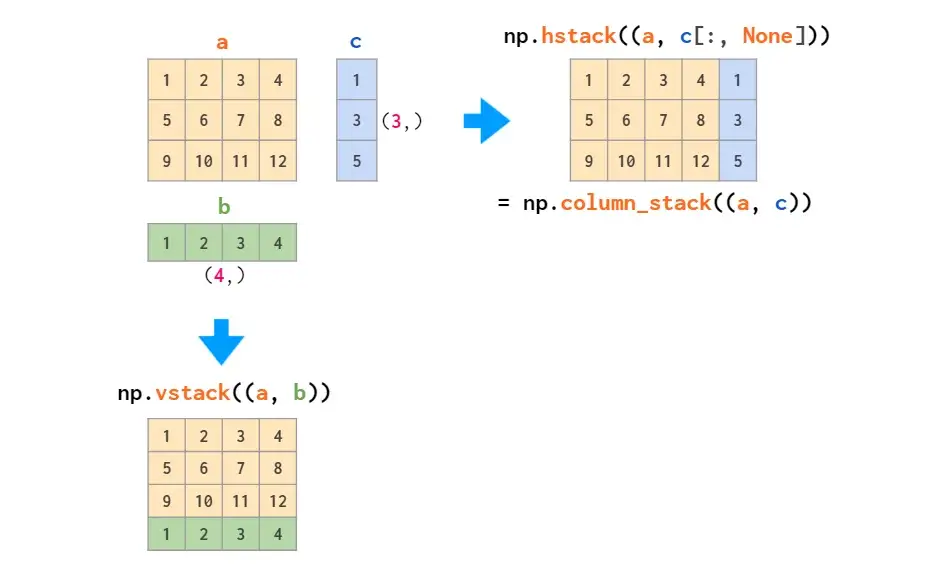
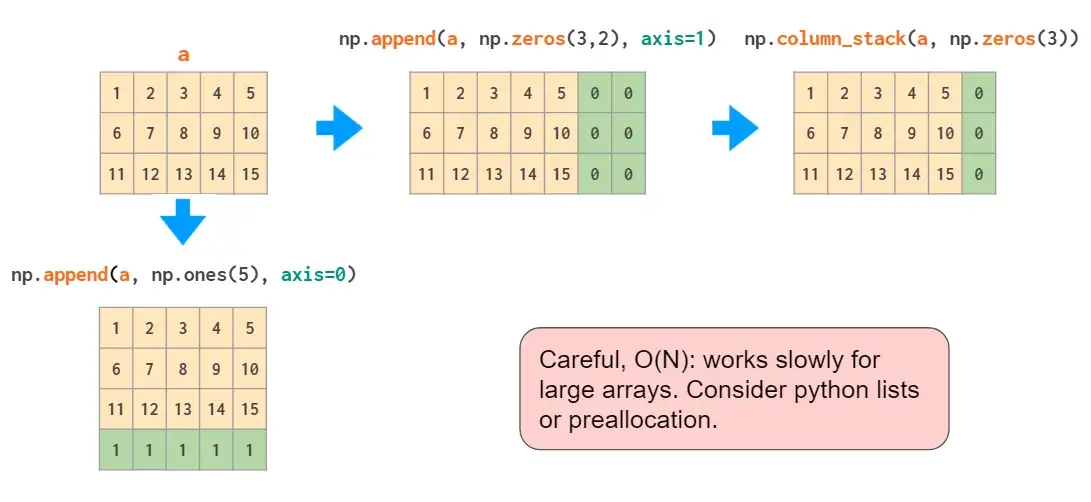
矩阵的拼接有以下两种方式:
图示操作仅适用于矩阵堆叠或向量堆叠,而一维数组和矩阵的混合堆叠只有通过vstack才可实现,hstack会导致维度不匹配错误。因为前文提到将一维数组作为行向量,而不是列向量。为此,可以将其转换为行向量,或使用专门的column_stack函数执行此操作:
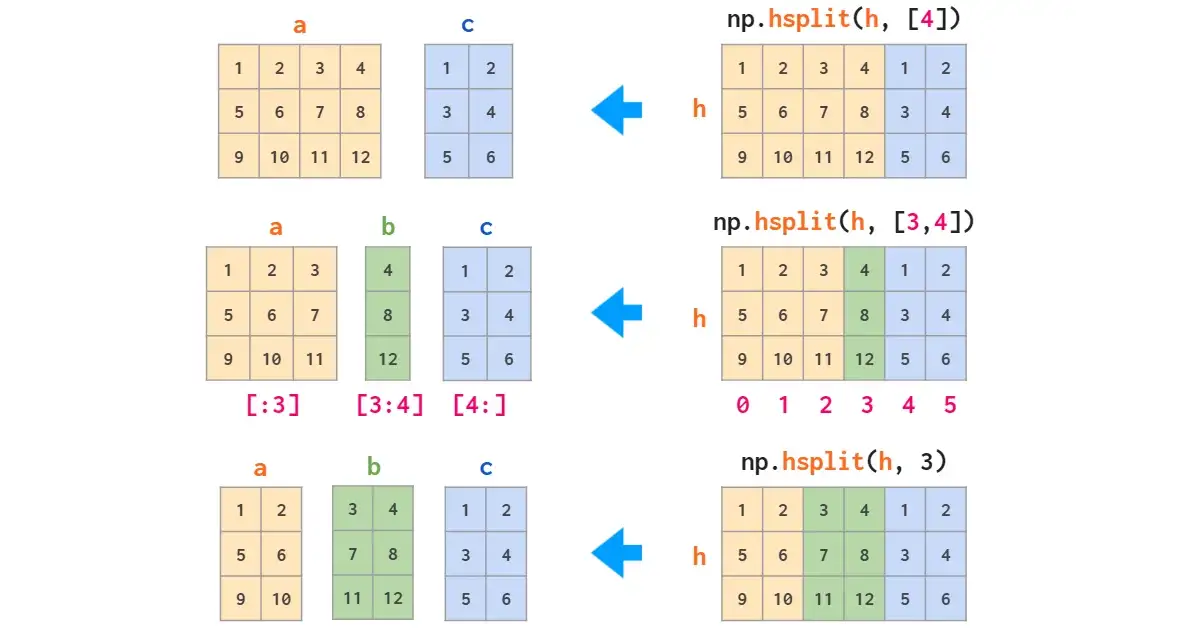
与stack对应的是split:
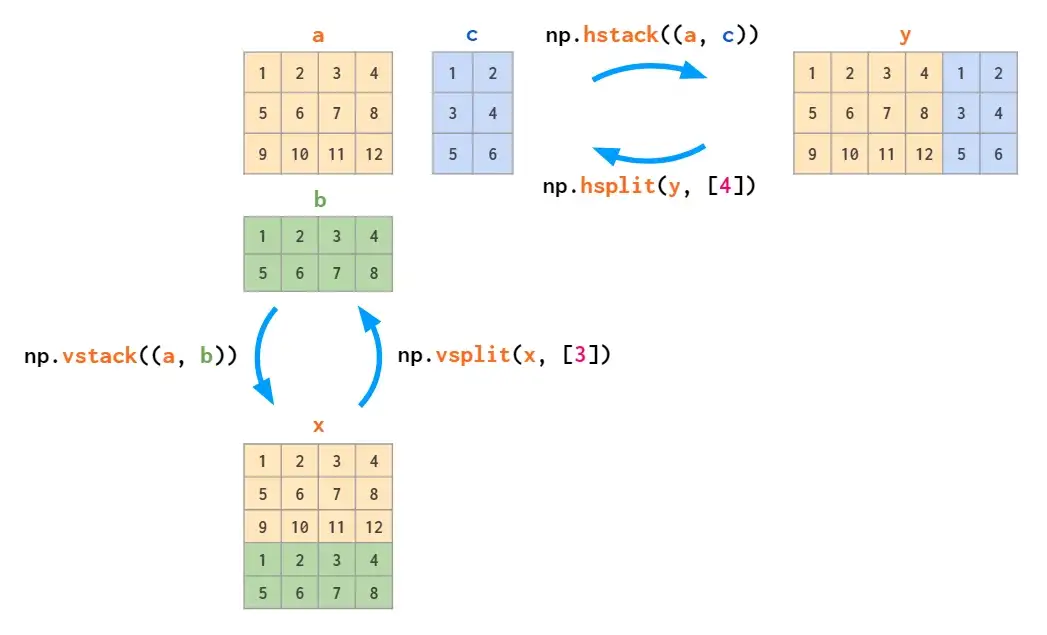
All split flavors accept either a list of indices to split at, or a single integer, the number of equal sized parts:
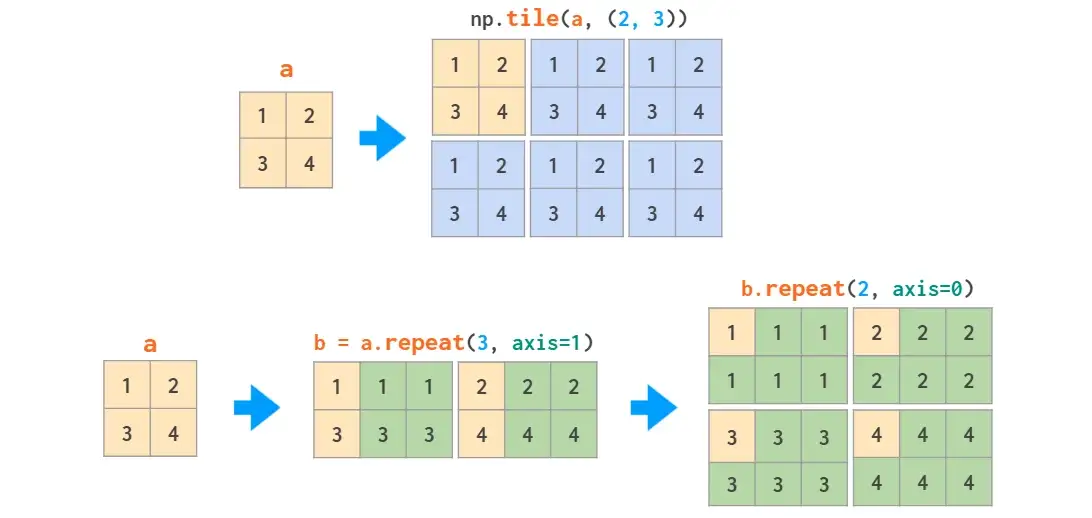
矩阵复制有两种方式:tile类似粘贴复制;repeat相当于分页打印。
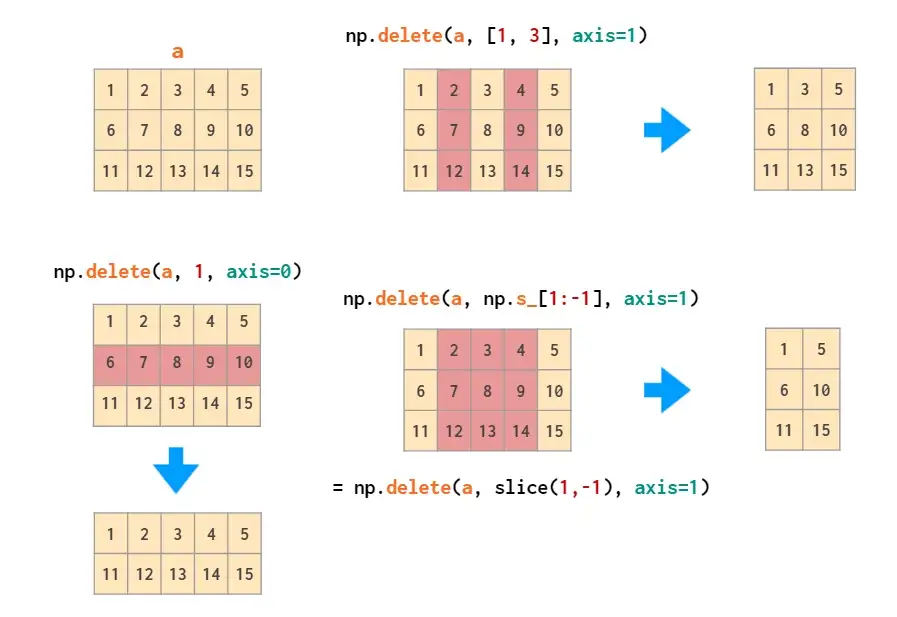
delete可以删除特定的行或列
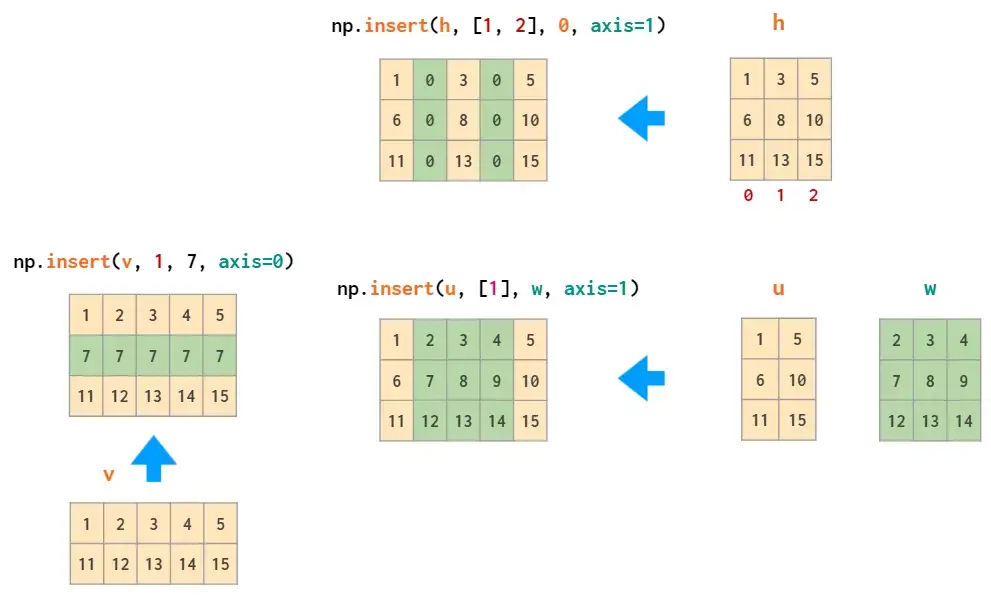
相应插入操作为insert:
与hstack一样,append函数无法自动转置1D数组,因此需要重新调整向量形状或添加维数,或者使用column_stack:
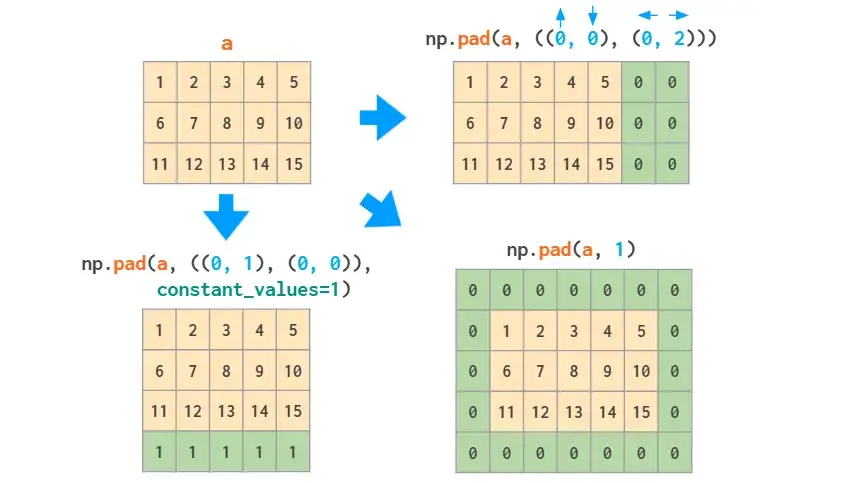
如果仅仅是向数组的边界添加常量值,pad函数是足够的:
6.Meshgrids
广播机制使得meshgrids变得容易。例如需要下图所示(但尺寸大得多)的矩阵:
上述两种方法由于使用了循环,因此都比较慢。MATLAB通过构建meshgrid处理这种问题。
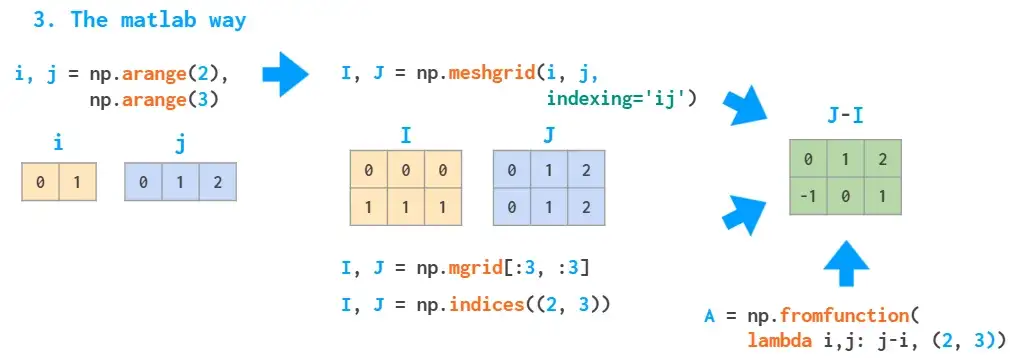
meshgrid函数接受任意一组索引,通过mgrid切片和indices索引生成完整的索引范围,然后,fromfunction函数根据I和J实现运算。
在NumPy中有一种更好的方法,无需在内存中存储整个I和J矩阵(虽然meshgrid已足够优秀,仅存储对原始向量的引用),仅存储形状矢量,然后通过广播规实现其余内容的处理:

如果没有indexing ='ij'参数,那么meshgrid将更改参数的顺序,即J,I=np.meshgrid(j,i)——一种用于可视化3D绘图的“ xy”模式(祥见该文档)。
除了在二维或三维网格上初始化函数外,网格还可以用于索引数组:
以上方法在稀疏网格中同样适用。
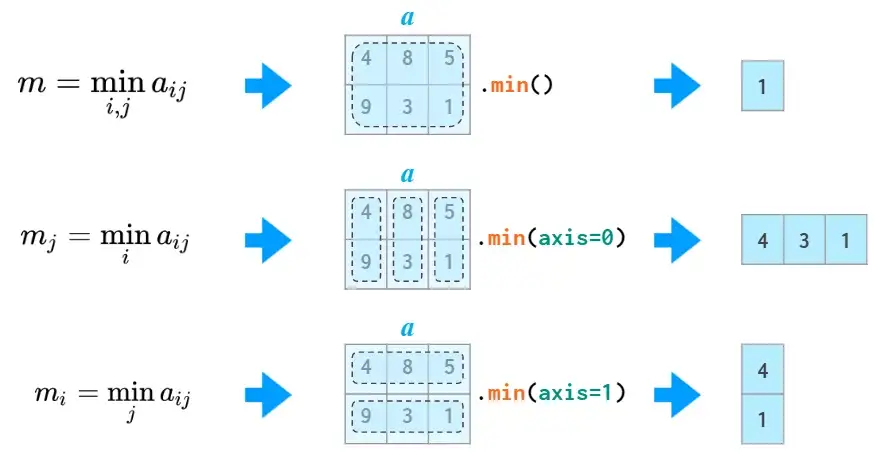
7.矩阵的统计
就像sum函数,numpy提供了矩阵不同轴上的min/max, argmin/argmax, mean/median/percentile, std/var等函数。
np.amin等同于np.min,这样做同样是为了避免from numpy import *可能的歧义。
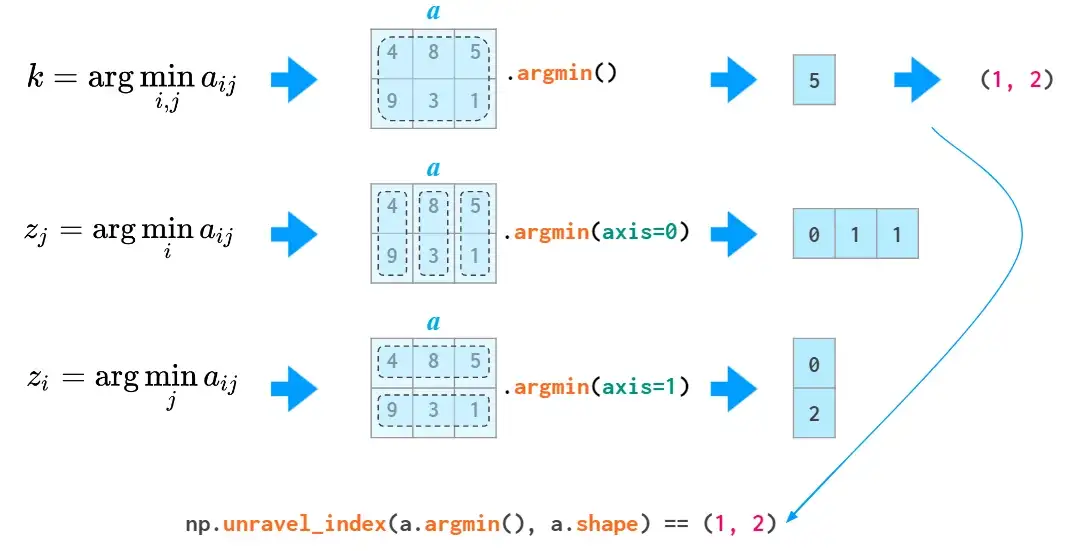
2维及更高维中的argmin和argmax函数分别返回最小和最大值的索引,通过unravel_index函数可以将其转换为二维坐标:
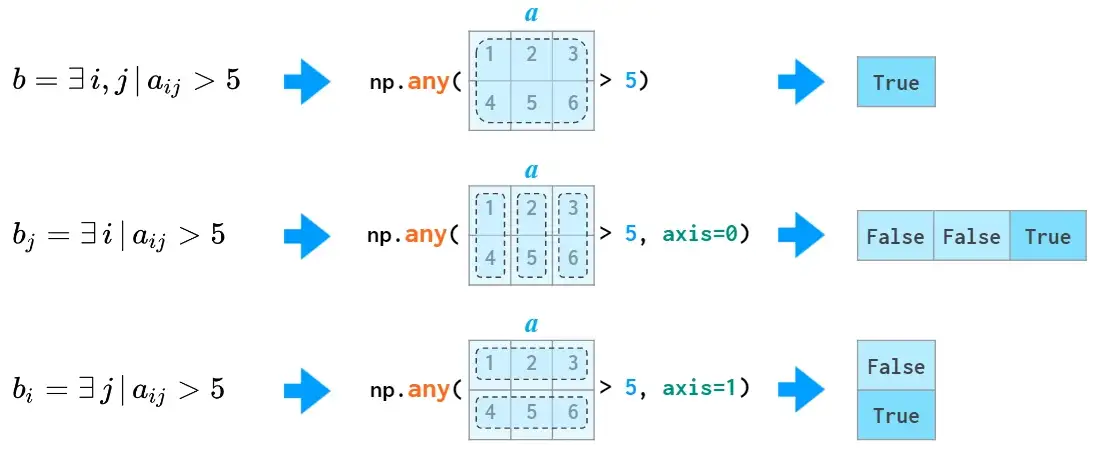
all和any同样也可作用于特定维度:
8.矩阵排序
虽然在一维数组中,axis参数适用于不同函数,但在二维数组排序中影响较小:

你通常不需要上述这样的排序矩阵,axis不是key参数的替代。但好在NumPy提供了其他功能,这些功能允许按一列或几列进行排序:
1、a[a[:,0].argsort()]表示按第一列对数组进行排序:
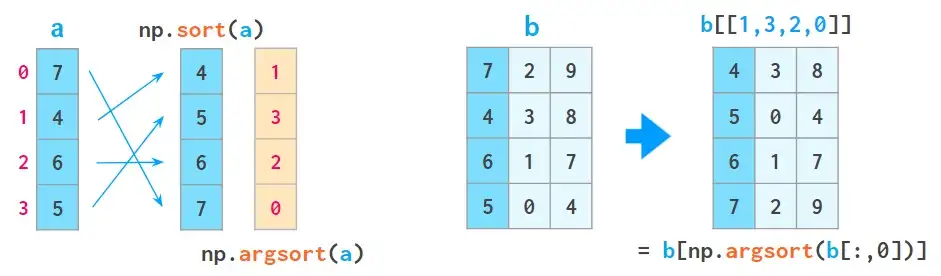
其中,argsort返回排序后的原始数组的索引数组。
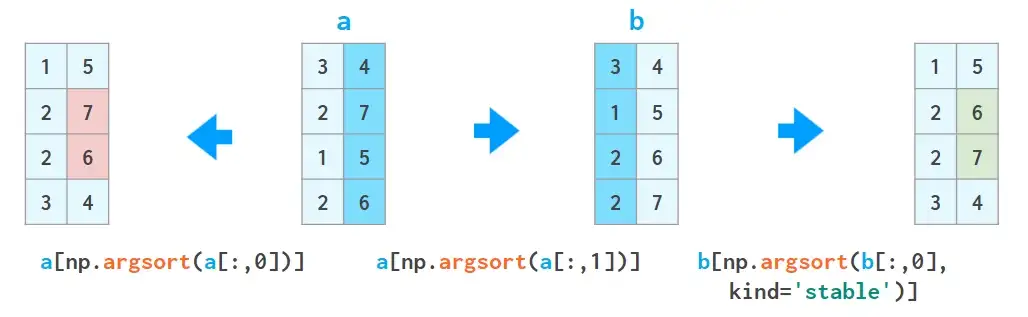
可以重复使用该方法,但千万不要搞混:
a = a[a[:,2].argsort()]
a = a[a[:,1].argsort(kind='stable')]
a = a[a[:,0].argsort(kind='stable')]
2、函数lexsort可以像上述这样对所有列进行排序,但是它总是按行执行,并且排序的行是颠倒的(即从下到上),其用法如下:
a[np.lexsort(np.flipud(a[2,5].T))],首先按第2列排序,然后按第5列排序;a[np.lexsort(np.flipud(a.T))],从左到右依次排序各列。
其中,flipud沿上下方向翻转矩阵(沿axis = 0方向,与a [::-1,...]等效,其中...表示“其他所有维度”),注意区分它与fliplr,fliplr用于1维数组。
3、sort函数还有一个order参数,但该方法极不友好,不推荐学习。
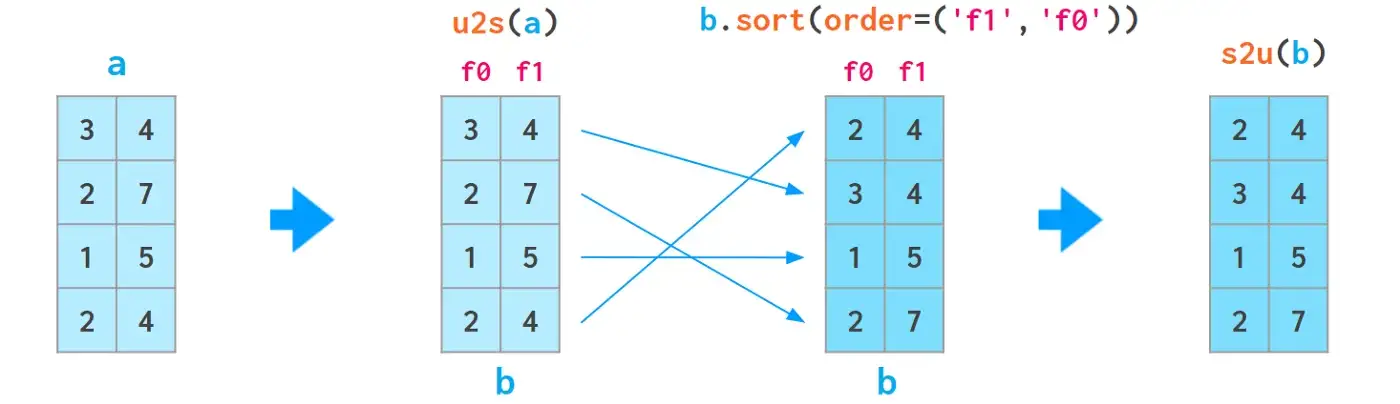
To use the order argument of sort, first convert the array to structured form, then sort it, and finally convert it back to the plain (‘unstructured’) form:
Both conversions are actually views, so they are fast and don’t require any extra memory. But the functions u2s and s2u need to be imported first with the horrific from numpy.lib.recfunctions import unstructured_to_structured as u2s, structured_to_unstructured as s2u
4、在pandas中排序也是不错的选择,因为在pandas中操作位置确定,可读性好且不易出错:
pd.DataFrame(a).sort_values(by=[2,5]).to_numpy(),先按第2列排序,再按第5列排序。
pd.DataFrame(a).sort_values().to_numpy(),按从左到右的顺序对所有列进行排序。