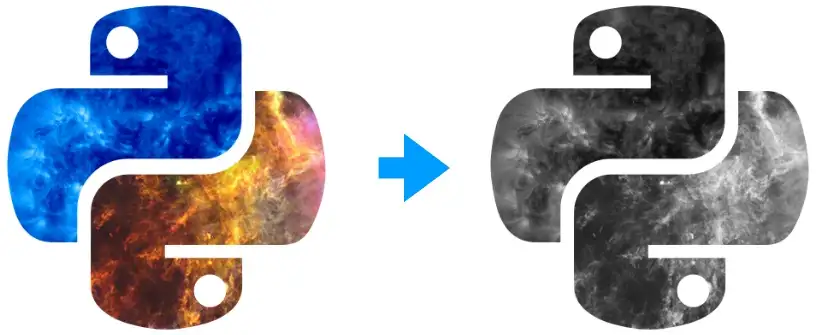5. 广播(Broadcast)

本文参考:

1. Broadcasting in NumPy

1. 什么是广播?

广播可以简单理解为用于不同大小数组的二进制通用函数(加、减、乘等)的一组规则。这是一个非常强大的功能，但是通常较难理解。 当数组大小彼此不匹配的时候，我们通常会从错误消息中看到广播的存在。

最简单的广播示例是n维数组乘以标量，这显然意味着该数组的所有元素乘以标量值：

广播类似于众所周知的类型提升：在大多数编程语言中，一个整数和一个浮点数进行运算时，整数会首先自动转换为浮点数类型。

在二维数组中（例如，将矩阵除以向量），广播有点棘手，因为操作的结果取决于操作数的特定形状：

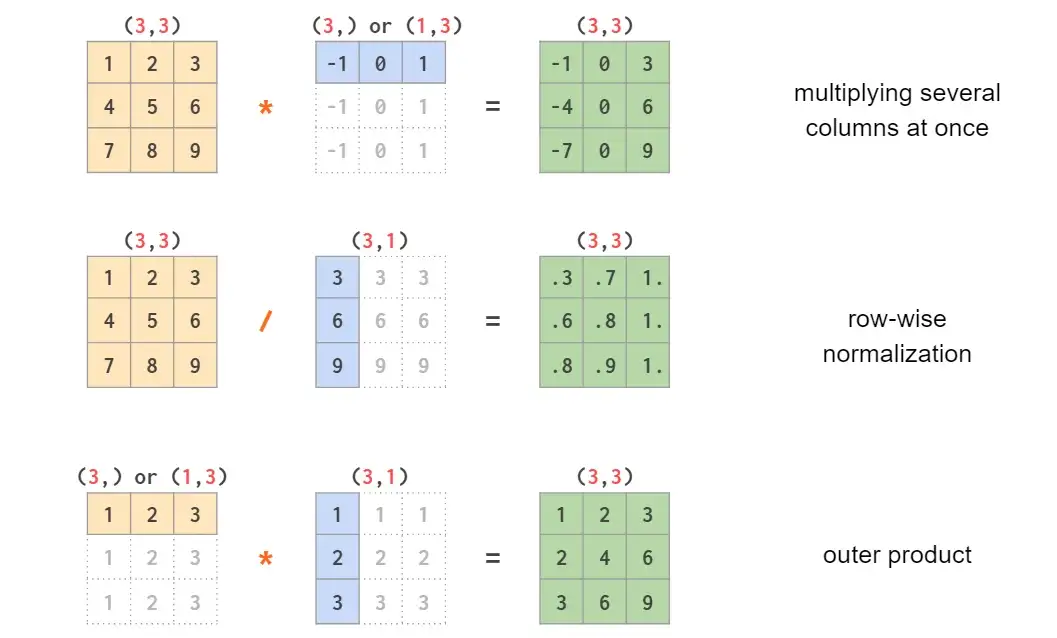
在三维数组及更高维度的数组中，广播甚至更不直观，使用它需要了解通用形式的广播规则。

2. 广播的规则

在NumPy三维以上中，广播机制很不直观，甚至很难直白的理解，因此使用它需要了解通用形式的广播规则，而NumPy的广播遵循证实遵循着一组严格的规则。

caution

• 规则一：如果两个数组的维度数不相同，那么小维度数组的形状将会在最左边补1。
• 规则二：如果两个数组的形状在任何一个维度上都不匹配，那么数组的形状会沿着维度为1的维度扩展以匹配另外一个数组的形状。
• 规则三：如果两个数组的形状在任何一个维度上都不匹配并且没有任何一个维度等于1，那么会引发异常。 来源于 -- 《Python Data Science Handbook》

根据规则之前三维数组的案例可解释如下：

为了更清楚地理解这些规则，来看几个具体的示例。

示例1

import numpy as np

M = np.ones((2, 3))
a = np.arange(3)

print(M + a)
print(M.shape)
print(a.shape)

[[1. 2. 3.]
 [1. 2. 3.]]
(2, 3)
(3,)

tip

M.shape = (2, 3)

a.shape = (3,)

可以看到，根据规则1， 数组a的维度数更小，所以在其左边补1：

tip

M.shape -> (2, 3)

a.shape -> (1, 3)

根据规则2， 第一个维度不匹配，因此拓展这个维度以匹配数组：

tip

M.shape -> (2, 3)

a.shape -> (2, 3)

示例2

import numpy as np

a = np.arange(3).reshape((3, 1))
b = np.arange(3)

print(a + b)
print(a.shape)
print(b.shape)

规则1告诉我们，需要用1将b的形状补全:

tip

a.shape -> (3, 1)

b.shape -> (1, 3)

规则2告诉我们，需要更新这两个数组的维度来互相匹配:

tip

a.shape -> (3, 3)

b.shape -> (3, 3)

因为结果匹配，所以这两个形状是兼容的，可以看到一下结果:

[[0 1 2]
 [1 2 3]
 [2 3 4]]
(3, 1)
(3,)

示例3

现在来看一个两组不兼容的示例:

import numpy as np

M = np.ones((3, 2))
a = np.arange(3)

print(M + a)

和第一个示例相比，这里有个微小的不同之处： 矩阵M是转置的。那么这将如何影响计算呢？两个数组的形状如下:

tip

M.shape = (3, 2)

a.shape = (3,)

规则1告诉我们，a数组的形状必须用1进行补全：

tip

M.shape -> (3, 2)

a.shape -> (1, 3)

根据规则2，a数组的第一个维度进行扩展以匹配M的维度：

tip

M.shape -> (3, 2)

a.shape -> (3, 3)

现在需要用到规则3——最终的形状还是不匹配，因此这两个数组是不兼容的。当我们执行运算时会看到以下结果：

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
Cell In[5], line 6
      3 M = np.ones((3, 2))
      4 a = np.arange(3)
----> 6 print(M + a)

ValueError: operands could not be broadcast together with shapes (3,2) (3,) 

danger

请注意，这里可能发生的混淆在于：

你可能想通过在a数组的右边补1，而不是左边补1，让a和M的维度变得兼容。但是这不被广播的规则所允许。

3. 实际案例

将彩色图像转换为灰度图像是三维数组广播的一个很好的例子。根据sRGB颜色空间的公式：

$$Y_{linear} = 0.2126 \times R_{linear} + 0.7152 \times G_{linear} + 0.0722 \times B_{linear}$$

可以通过图像颜色通道的线性组合获得亮度。使用广播的策略，代码可以写成如下：

gray = np.sum(im*[0.2126, 0.7152, 0.0722], axis=2)

其中im是一张RGB标准图片的数组值，

im.shape == (1080, 1920, 3)

gray.shape == (1080, 1920)

1080是图片的高度， 1920是图片的宽度，3是图片RGB的三个通道。 (关于图片的格式，请阅读图像格式RGB/HSV/YUV)

完整代码如下：

import numpy as np
from matplotlib.pyplot import imread, imsave

a = imread('python-logo.png')
b = np.sum(a*[0.2126, 0.7152, 0.0722], axis=2)
imsave('logo-gray.png', b, cmap='gray')

原始图片地址：http://openastronomy.org/pyastro/logo/

执行灰度操作以后的效果：