Skip to main content

实验6: 常微分方程数值解实验

问题1：欧拉法和改进欧拉法求常微分方程初值问题数值解​

问题1：分别编写Euler方法和改进的Euler方法计算常微分方程初值问题的数值解程序。分别取步长h=0.1,0.05h=0.1, 0.05来计算下面的初值问题，并画图比较计算效果（解析解为y=1+2xy=\sqrt{1+2x}）。

{y′(x)=y−2xy,x∈[0,1]y(0)=1\begin{cases} y'(x) = y - \dfrac{2x}{y}, x\in[0, 1]\\ y(0) = 1 \end{cases}

实验原理：考虑一阶常微分方程(组)的初值问题(Initial Value Problem, IVP)

{y′(x)=f(x,y),x∈[a,b]y(a)=y0.\begin{equation*} \left\{ \begin{split} & y'(x)=f(x,y), x\in [a,b] \\ & y(a)=y_0. \end{split} \right. \end{equation*}

对区间[a,b][a, b]进行NN等分，步长h=b−aNh= \dfrac{b-a}{N}, 离散节点为xn=a+nh,n=0,1,⋯ ,N.x_n=a+nh, n=0,1,\cdots, N.

  • 欧拉(Euler)公式为
    yn+1=yn+hf(xn,yn),  n=0,1,⋯ ,N−1y_{n+1}=y_n+h f(x_n,y_n),~~n=0,1,\cdots,N-1
  • 改进欧拉公式为
    {yˉn+1=yn+hf(xn,yn),predictionyn+1=yn+h2[f(xn,yn)+f(xn+1,yˉn+1)].correction\left\{ {\begin{array}{lr} {\color{red}\bar y_{n+1}}=y_n+hf(x_n,y_n),&\text{prediction}\\ \\ y_{n+1}=y_n+\dfrac{h}{2}[f(x_n,y_n)+f(x_{n+1},{\color{red}\bar y_{n+1}})].&\text{correction}\end{array}}\right.
    为了便于编程，改进欧拉公式常改写为
    {k1=f(xn,yn),k2=f(xn+h,yn+hk1)yn+1=yn+h(12k1+12k2),,n=0,1,⋯ ,N−1\begin{cases} {\color{red}k_1}=f(x_n,y_n),\\ {\color{red}k_2}=f(x_n+h,y_n+hk_1)\\ y_{n+1}=y_n+h\left(\dfrac{1}{2}{\color{red}k_1}+\dfrac{1}{2}{\color{red}k_2}\right),&\\ \end{cases}, n=0,1,\cdots,N-1

实验过程：

'''
欧拉法和改进欧拉法求ODE初值问题数值解
'''
import numpy as np
import matplotlib.pyplot as plt
# #绘图显示中文
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

#欧拉法
def Euler(f, a, b, y0, h):
    '''
    :param f: y'(x) = f(x, y)
    :param a: 区间[a, b]
    :param b:
    :param y0: 初始值y(a) = y0
    :param h: 步长
    :return: 数值解[X, Y]
    '''
    N = round((b-a)/h)  #区间等分数
    X = np.linspace(a, b, N+1).reshape((-1, 1)) #离散节点，转化为列向量
    Y = np.zeros_like(X)
    Y[0] = y0 #初始值
    for n in range(N):
        '''
        ------------------------------
        这里作为作业思考，请根据你的理解补充完整
        ------------------------------
        '''

    return X, Y

#改进欧拉法
def improved_Euler(f, a, b, y0, h):
    '''
    :param f: y'(x) = f(x, y)
    :param a: 区间[a, b]
    :param b:
    :param y0: 初始值y(a) = y0
    :param h: 步长
    :return: 数值解[X, Y]
    '''
    N = round((b-a)/h)  #区间等分数
    X = np.linspace(a, b, N+1).reshape((-1, 1)) #离散节点，转化为列向量
    Y = np.zeros_like(X)
    Y[0] = y0 #初始值
    '''
    ------------------------------
    这里作为作业思考，请根据你的理解补充完整
    ------------------------------
    '''
    
#定义微分函数
def f(x, y):
    return y - 2 * x / y

# y'(x) = f(x, y)的解析解
def exact_solution(x):
    return np.sqrt(1 + 2 * x)

#计算误差和观察数值解效果
def plotting_Euler_result(f, a, b, y0, h_list):
    '''
    :param f: y'(x) = f(x, y)
    :param a: 区间[a, b]
    :param b:
    :param y0: 初始值y(a) = y0
    :param h_list: 步长
    '''
    for h in h_list:
        X1, Y1 = Euler(f=f, a=a, b=b, y0=y0, h=h)
        Y_exact = exact_solution(X1)
        error1 = Y_exact - Y1  #欧拉方法误差
        result = np.hstack((X1, Y1)) #保存结果到result
        result = np.hstack((result, error1))
        plt.plot(X1, Y1, 'o', markersize=2, linewidth=2, label=f'Euler方法h={h}')

        '''
        利用改进欧拉法求数值解
        ------------------------------
        这里作为作业思考，请根据你的理解补充完整
        ------------------------------
        '''
        result = np.hstack((result, Y2))
        result = np.hstack((result, error2))
        result = np.hstack((result, Y_exact))
        #输出结果到csv文件，用excel可打开显示
        np.savetxt('Euler-result_h=' + str(h) + '.csv',
                   result,
                   header='离散节点, Euelr法数值解, Euler法误差, 改进Euler数值解, 改进Euler法误差, 解析解',
                   fmt='%10.8f',
                   delimiter=',')

        plt.plot(X2, Y2, 'd', markersize=2, linewidth=2, label=f'改进Euler方法h={h}')

    #绘制解析解
    xdata = np.linspace(a, b, 100)
    ydata = exact_solution(xdata)
    plt.plot(xdata, ydata, '-', markersize=2, linewidth=2, label='解析解')

    plt.xlabel('x')
    plt.ylabel('y')
    plt.title('Euler方法和改进Euler方法求ODE的数值解')
    plt.legend()
    plt.savefig('Euler_result.svg', dpi=500)
    plt.close()

    #绘制误差曲线
    plt.plot()
    plt.plot(X1, abs(error1), '--o', markersize=4, linewidth=2, label=f'Euler方法取h={h}时的绝对误差')
    '''
    ------------------------------
    这里作为作业思考，请根据你的理解补充完整
    ------------------------------
    '''
    plt.close()


if __name__ == '__main__':
    a = 0 #区间[a, b]
    b = 1.0
    y0 = 1.0 #初始值
    h_list = [0.1, 0.05]  #步长列表
    plotting_Euler_result(f=f, a=a, b=b, y0=y0, h_list=h_list)

输出结果为Euler_result

图1: Euler和改进Euler方法求解常微分方程数值解效果

error_result_h=0.05

图2: Euler和改进Euler方法求解常微分方程数值解绝对误差

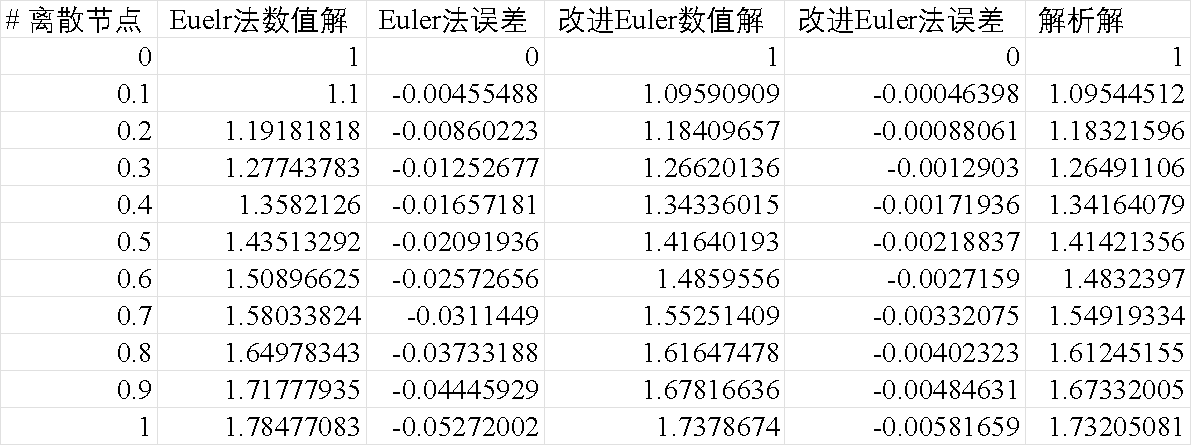
image-20221218172108721

图3: h=0.1时，Euler和改进Euler方法保存到csv文件的数值解结果

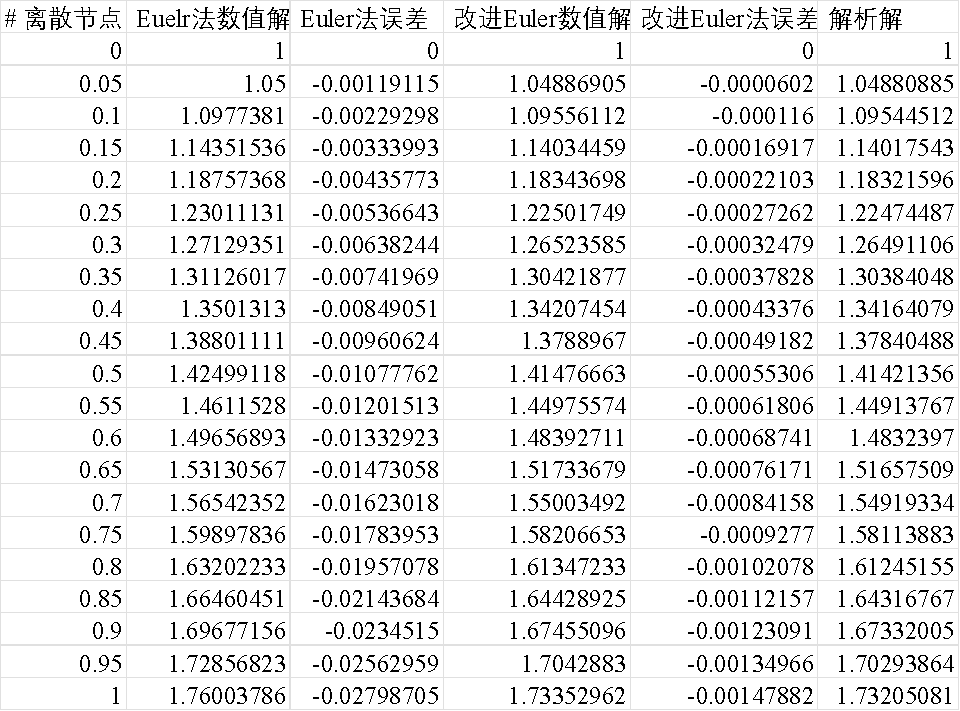
image-20221218172327423

图4: h=0.05时，Euler和改进Euler方法保存到csv文件的数值解结果

问题2：龙格-库塔(Runge-Kutta)法求常微分方程初值问题数值解​

问题2：编写经典四阶龙格-库塔公式计算常微分方程初值问题的数值解程序。并分别取步长h=0.1,0.05h=0.1, 0.05来计算问题1中微分方程初值问题的数值解。并画图比较计算效果。

实验原理：考虑一阶常微分方程(组)的初值问题(Initial Value Problem, IVP)

{y′(x)=f(x,y),x∈[a,b]y(a)=y0.\begin{equation*} \left\{ \begin{split} & y'(x)=f(x,y), x\in [a,b] \\ & y(a)=y_0. \end{split} \right. \end{equation*}

对区间[a,b][a, b]进行NN等分，步长h=b−aNh= \dfrac{b-a}{N}, 离散节点为xn=a+nh,n=0,1,⋯ ,N.x_n=a+nh, n=0,1,\cdots, N.

  • 四阶经典龙格-库塔(Runge-Kutta)格式为
    {k1=f(xn,yn),k2=f(xn+12h,yn+12hk1),k3=f(xn+12h,yn+12hk2),k4=f(xn+h,yn+hk3)yn+1=yn+16h(k1+2k2+2k3+k4),,  n=0,1,⋯ ,N−1\begin{cases} {\color{red}k_1}=f(x_n,y_n),\\ {\color{red}k_2}=f\left(x_n+\dfrac{1}{2}h,y_n+\dfrac{1}{2}hk_1\right),\\ {\color{red}k_3}=f\left(x_n+\dfrac{1}{2}h,y_n+\dfrac{1}{2}hk_2\right),\\ {\color{red}k_4}=f(x_n+h,y_n+hk_3)\\ y_{n+1}=y_n+\dfrac{1}{6}h({\color{red}k_1+2k_2+2k_3+k_4}),\\ \end{cases},~~n=0,1,\cdots,N-1

实验原理：请自己动手实践和探讨对结果的分析。

问题3：一阶常微分方程组初值问题数值解​

一阶微分方程组IVP：

{y1′(x)=f1(x,y1(x),⋯ ,ym(x)),⋯ ,ym′(x)=fm(x,y1(x),⋯ ,ym(x)),y1(x0)=y10,⋯ ,ym(x0)=ym0.\begin{equation*} \left\{ \begin{split} y_1'(x) & =f_1(x, y_1(x), \cdots, y_m(x)), \\ & \cdots , \\ y_m'(x) & =f_m(x, y_1(x), \cdots, y_m(x)), \\ y_1(x_0) & =y_1^0, \\ &\cdots,\\ y_m(x_0) & =y_m^0. \end{split} \right. \end{equation*}

上述微分方程组改写成向量形式：令 Y=(y1⋮ym)Y=\begin{pmatrix} y_1 \\ \vdots \\ y_m \\ \end{pmatrix}, F=(f1⋮fm)F=\begin{pmatrix} f_1 \\ \vdots \\ f_m \\ \end{pmatrix}, Y0=(y10⋮ym0)Y_0=\begin{pmatrix} y_1^0 \\ \vdots \\ y_m^0 \\ \end{pmatrix}, 则向量形式为

{Y′(x)=F(x,Y),Y(x0)=Y0\begin{equation*} \left\{ \begin{split} Y'(x) & =F(x,Y), \\ Y(x_0) &= Y_0 \end{split} \right. \end{equation*}

3.1 实例：传染病SIR模型及其数值求解​

3.1.1 模型建立​

天花、麻疹等传染病有免疫性，将人群分为三类：已感染者（Infective）、易感染者（Susceptible）和移出者（Removed）. 记tt时刻三类病人所占的比例分别为i(t)i(t), s(t)s(t), r(t)=1−i(t)−s(t)r(t) = 1- i(t) - s(t).

设病人的日接触率为λ\lambda, 日治愈率为μ\mu，可建立i(t),s(t)i(t), s(t)所满足的一阶微分方程组

{di(t)dt=λs(t)i(t)−μi(t),ds(t)dt=−λs(t)i(t),t∈[0,T]i(0)=i0,s(0)=s0\begin{equation*} \left\{ \begin{split} \frac{di(t)}{dt} & =\lambda s(t)i(t)- \mu i(t), \\ \frac{ds(t)}{dt} & =-\lambda s(t)i(t), t\in[0, T] \\ i(0) & =i_0, s(0)=s_0 \end{split} \right. \end{equation*}

3.1.2 模型的数值格式​

传染病SIR模型的欧拉格式数值求解：类似前面的讨论，可建立如下格式

{in+1=in+dt(λsnin−μin),sn+1=sn−dtλsnin,n=0,1,⋯ ,N−1i0,s0\begin{equation*} \left\{ \begin{split} i_{n+1} & =i_n+ dt(\lambda s_n i_n - \mu i_n), \\ s_{n+1} & =s_n -dt \lambda s_n i_n, n=0,1,\cdots, N-1\\ i_0, & s_0 \\ \end{split} \right. \end{equation*}

3.1.3 算例结果​

请根据上面的迭代格式自己动手编程实现，取T=50T=50，i0=0.02,s0=0.98,λ=1,μ=0.3i_0=0.02, s_0 = 0.98, \lambda = 1, \mu = 0.3，绘图展示三类人的动态变化曲线，以及s−is-i的相平面曲线，结果可以参考下面的图5和图6.

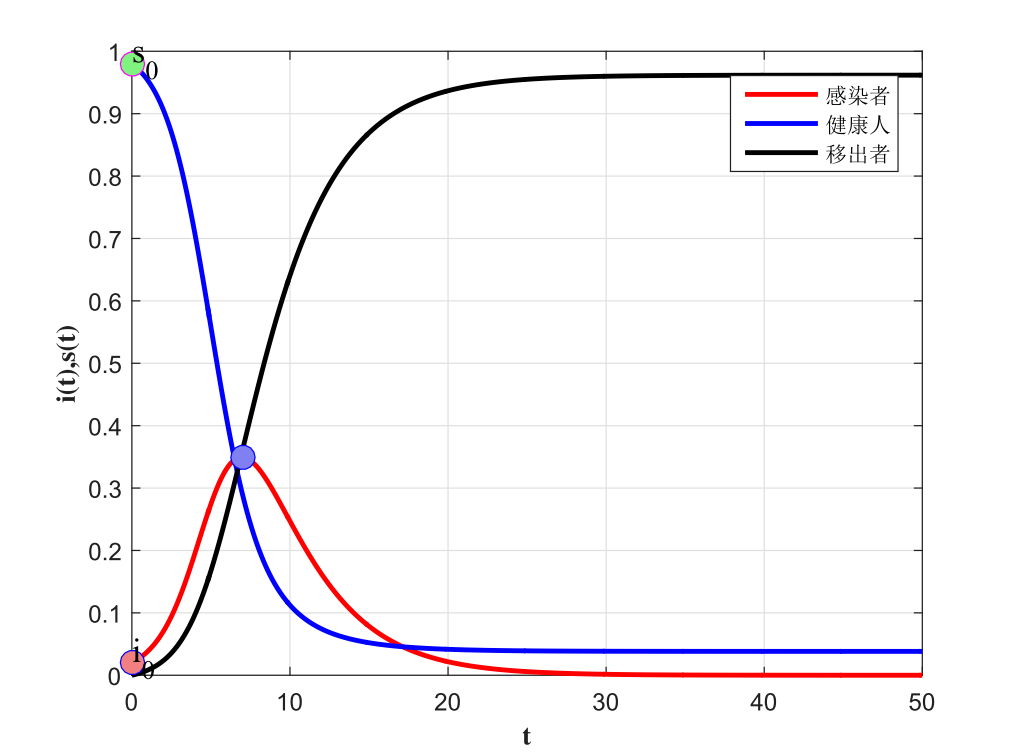
image-20221218195210920

​ 图5：i0=0.02,s0=0.98,λ=1,μ=0.3i_0=0.02, s_0 = 0.98, \lambda = 1, \mu = 0.3的三类人的动态变化曲线

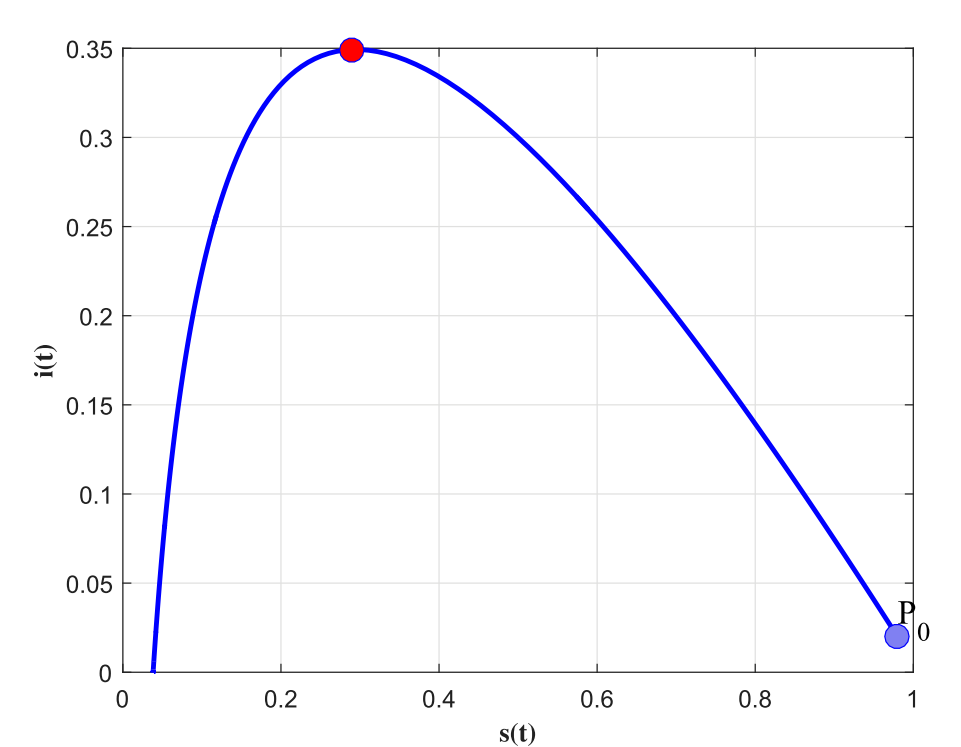
image-20221218195437015.png

​ 图6：i0=0.02,s0=0.98,λ=1,μ=0.3i_0=0.02, s_0 = 0.98, \lambda = 1, \mu = 0.3的ss-ii的相平面曲线

3.1.4 利用scipy的odeint函数的结果检验​

SciPy 的 integrate 模块提供了一个 ODE 求解器接口:integrate.odeint.

odeint 函数是 ODEPACK的 LSODA 求解器的一个接口，它可以自动在（用于非刚性问题的）Adams 预测-校正方法和（用于刚性问题的）BDF 方法之间切换。

odeint函数有三个强制性参数：

  • 用于评估标准形式 ODE 右侧的函数
  • 指定未知函数初始条件的数组（或标量）
  • 具有自变量的数组，其中未知函数要被计算。

具体使用步骤可以参考下面的算例。

'''
利用scipy.integrate的odeint函数求传染病SIR模型的数值解
'''
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
# #绘图显示中文
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 编写SIR模型函数
# i'(t) = f1(t, i, s)
# s'(t) = f2(t, i, s)
def SIR(Y, t, alpha):
    '''
    :param Y: 因变量列表Y = [i(t), s(t)], 已感染者Infective, 易感染者Susceptible
    :param t: 自变量
    :param alpha: 参数列表
    :return: Y'(t) = F(t, Y)的函数关系
    '''
    i, s = Y
    lmda, mu = alpha
    di = lmda * s * i - mu * i
    ds = -lmda * s * i
    return np.array([di, ds])

def SIR_main():
    T = 50 #时间长度
    t_data = np.linspace(0, T, 200) #离散时间节点
    Y0 = (0.02, 0.98) #tuple, Y的初始值，病人占比0.02，健康人占比0.98
    alpha = (1.0, 0.3)  #tuple, 模型参数lmda = 1, mu =0.3
    Y = odeint(func=SIR, y0=Y0, t=t_data, args=(alpha, ))
    i_data = Y[:, 0]  #i(t)的数值解
    s_data = Y[:, 1]  #s(t)的数值解
    r_data = 1 - i_data - s_data #移出者动态比例
    i_max = max(i_data)  #最大值
    i_data = i_data.tolist()  #转化为list
    max_index = i_data.index(i_max)  #找到列表最大值的位置
    t_max = t_data[max_index]        #感染者达到最大值的时刻
    s_max = s_data[max_index]        #感染者达到最大值对应的健康人的比例
    
    #绘图展示三类人的变化趋势
    fig = plt.figure()
    plt.plot(t_data, i_data, '-', linewidth=2, label='感染者$i(t)$')
    plt.plot(t_data, s_data, '-', linewidth=2, label='健康者$s(t)$')
    plt.plot(t_data, r_data, '-', linewidth=2, label='移出者$r(t)$')
    plt.plot(t_data[0], s_data[0], 'o')
    plt.plot(t_data[0], i_data[0], 'o')
    plt.plot(t_data[0], r_data[0], 'o')
    plt.plot(t_max, i_max, 'rs', markersize=6, label='感染者最大比例')

    plt.xlabel('$t$')
    plt.ylabel('三类人的比例')
    plt.legend()
    plt.savefig('SIR-result1.svg', dpi=500)
    plt.close()

    #绘制i-s相平面图
    plt.plot(s_data, i_data, linewidth=2, label='$i-s$曲线')
    plt.plot(s_max, i_max, 'ro', markersize=6, label='感染者峰值')
    plt.plot(s_data[0], i_data[0], 'o', color='purple', markersize=6, label='初始状态')
    plt.xlabel('$s(t)$')
    plt.ylabel('$i(t)$')
    plt.legend()
    plt.savefig('SIR-result2.svg', dpi=500)
    plt.close()

if __name__ == '__main__':
    SIR_main()

类似可以得到三类人的动态变化曲线以及相平面图，见图7和图8.

lab6-SIR-result1

​ 图7：scipy实现的i0=0.02,s0=0.98,λ=1,μ=0.3i_0=0.02, s_0 = 0.98, \lambda = 1, \mu = 0.3的三类人群的动态变化曲线

lab6-SIR-result2

​ 图8：scipy实现的i0=0.02,s0=0.98,λ=1,μ=0.3i_0=0.02, s_0 = 0.98, \lambda = 1, \mu = 0.3的ss-ii的相平面曲线

3.2 高阶微分方程化为一阶微分方程组​

Higher-Order Equations：

{y(n)(x)=f(x,y(x),y′(x),⋯ ,y(n−1)(x)),y(x0)=a0,y′(x0)=a1,⋯ ,y(n−1)(x0)=an−1\begin{equation*} \left\{ \begin{split} y^{(n)}(x) & =f(x, y(x), y'(x),\cdots, y^{(n-1)}(x)), \\ y(x_0) & =a_0, y'(x_0)=a_1, \cdots, y^{(n-1)}(x_0)=a_{n-1} \end{split} \right. \end{equation*}

引入新变量化为一阶微分方程组：令y1=y(x),y2=y′(x),⋯ ,yn=y(n−1)(x)y_1=y(x), y_2=y'(x), \cdots, y_n=y^{(n-1)}(x), 则

{y1′(x)=y2,⋯ ,yn−1′(x)=yn,yn′(x)=f(x,y1,y2,⋯ ,yn),y1(x0)=a0,⋯ ,yn(x0)=an−1.\begin{equation*} \left\{ \begin{split} y_1'(x) & =y_2, \\ & \cdots , \\ y_{n-1}'(x) & =y_n, \\ y_{n}'(x) & =f(x, y_1, y_2, \cdots, y_n), \\ y_1(x_0) & =a_0,\cdots, y_n(x_0)=a_{n-1}. \end{split} \right. \end{equation*}

问题4：有限差分法初步​

4.1 二阶常微分方程边值问题和有限差分格式​

{y′′(x)=f(x,y(x),y′(x)),x∈[a,b],y(a)=α,y(b)=β.\begin{equation*} \left\{ \begin{split} y''(x)& =f\left(x, y(x), y'(x)\right), x\in[a,b], \\ y(a) & =\alpha, \\ y(b) & =\beta. \end{split} \right. \end{equation*}

有限差分法（Finite Difference Method，FDM）：将求解区间[a,b][a, b]等分为NN份，取节点 xi=a+ih,x_i = a + ih, (i=0,1，⋯ ,N)(i = 0,1， \cdots, N )，利用数值微分在每一个节点处将 y′y'和 y′′y''离散化。上述边值问题可化为线性方程组

{yi+1−2yi+yi−1h2=f(xi,yi,yi+1−yi−12h),i=1,⋯ ,N−1y0=α,yN=β\begin{equation*} \left\{ \begin{split} &\frac{y_{i+1}-2y_i+y_{i-1}}{h^2} =f(x_i, y_i, \frac{y_{i+1}-y_{i-1}}{2h}), i=1,\cdots, N-1 \\ & y_0 =\alpha, \\ & y_N =\beta \\ \end{split} \right. \end{equation*}

4.2 算例和结果展示​

{y′′(x)=6x,x∈[0,1],y(0)=0,y(1)=0.\begin{equation*} \left\{ \begin{split} y''(x)& =6x, x\in[0, 1], \\ y(0) & =0, \\ y(1) & =0. \end{split} \right. \end{equation*}

FD格式为

{yi+1−2yi+yi−1h2=6xi,i=1,⋯ ,N−1y0=0,yN=0\begin{equation*} \left\{ \begin{split} &\frac{y_{i+1}-2y_i+y_{i-1}}{h^2} =6 x_i, i=1,\cdots, N-1 \\ & y_0 =0, \\ & y_N =0 \\ \end{split} \right. \end{equation*}

化为线性方程组为

(−210⋯01−21⋯0⋯⋯⋯⋯⋯0⋯1−210⋯01−2)(y1y2⋮yN−2yN−1)=(6h2x1−y06h2x2⋮6h2xN−26h2xN−1−yN)\begin{equation*} \begin{pmatrix} -2 & 1 & 0 & \cdots & 0 \\ 1 & -2 & 1 & \cdots & 0\\ \cdots & \cdots & \cdots & \cdots & \cdots\\ 0 & \cdots & 1 & -2 & 1 \\ 0 & \cdots & 0 & 1 & -2 \\ \end{pmatrix} \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_{N-2} \\ y_{N-1} \\ \end{pmatrix} =\begin{pmatrix} 6h^2x_1-y_0 \\ 6h^2x_2 \\ \vdots \\ 6h^2x_{N-2} \\ 6h^2x_{N-1}-y_N\\ \end{pmatrix} \end{equation*}

请动手编写程序，可与解析解y=x3−xy=x^3-x进行比较，数值解效果如下。

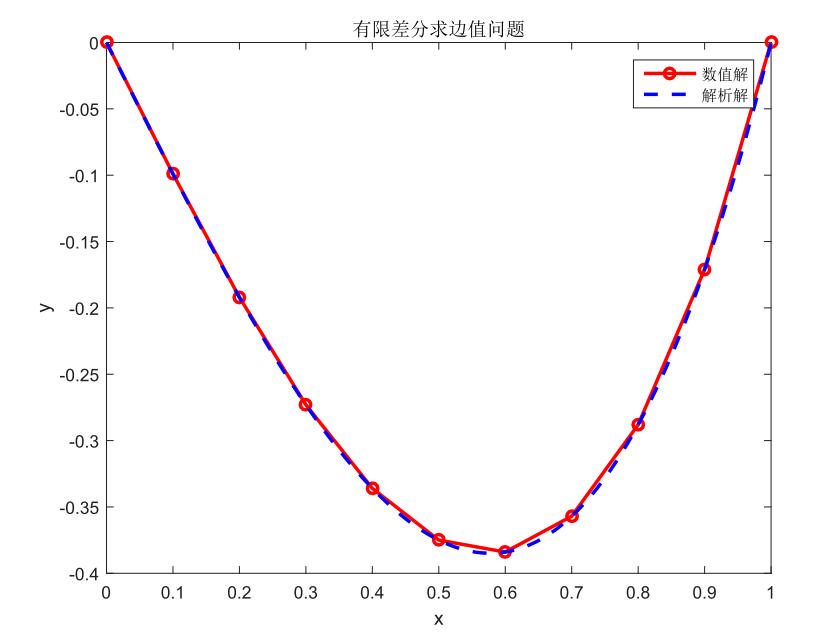
image-20221218200458270

图9：有限差分求解二阶常微分方程边值问题的数值解效果

问题5：热传导偏微分方程数值求解及应用​

数学建模应用案例中的“多层高温作业专业服装设计问题”、“炉温曲线机理建模与优化设计”等需要建立热传导微分方程及其边界条件、初始条件，可利用上面的有限差分法建立有限差分显格式和有限差分隐格式。

感兴趣的同学可以关注数学建模相关问题和应用。